ACTIVITY ON OSCILLATIONS
A body is performing a simple harmonic oscillation x(t) = A sin(w t), with width A = 10 cm and frequency w = 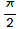 .
.
a) Calculate the position of the body 1, 2 and 3 sec from the starting time point the oscillation (the starting position regarded as 0).
b) Create the table of positions for the time points t = 0, 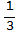 ,
, 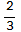 , 1,
, 1, 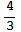 ,
, 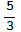 ,2,
,2, 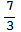 ,
, 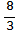 , 3,
, 3,  ,
, 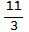 ,4sec
,4sec
c) Plot the graph of the position of the body in the time interval [0, T sec] where T = the smallest period.
Note: In order to define any function or run any program or command in Mathematica, press SHIFT + ENTER or ENTER in the Num Pad.
![x[t_] := A * Sin[w * t]](../HTMLFiles/Physics, Oscillations_10.gif)
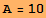



a) In order to calculate the body's position for t = 1 sec, t = 2 sec and t = 3 sec we are calculating the values of the function x(t) for t = 1, t = 2 and t = 3.
![x[1]](../HTMLFiles/Physics, Oscillations_15.gif)

![x[2]](../HTMLFiles/Physics, Oscillations_17.gif)
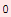
![x[3]](../HTMLFiles/Physics, Oscillations_19.gif)
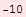
b) In order to create the table of positions for the time points t =0, 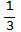 ,
, 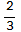 , 1,
, 1,  ,
,  ,2,
,2,  ,
,  , 3,
, 3,  ,
, 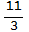 ,4 sec we are using the command Table[ {t, x [t] }, {t, 0, 4, 1/3} ]
,4 sec we are using the command Table[ {t, x [t] }, {t, 0, 4, 1/3} ]
![TableForm[Table[{t, x[t]}, {t, 0, 4, 1/3}], TableHeadings→ {None, {"t", "x(t)"}}, TableAlignments→Center, TableDirections→Row]](../HTMLFiles/Physics, Oscillations_29.gif)
| t |
0 |
 |
 |
1 |
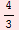 |
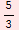 |
2 |
 |
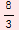 |
3 |
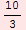 |
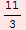 |
4 |
| x(t) |
0 |
5 |
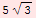 |
10 |
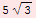 |
5 |
0 |
-5 |
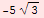 |
-10 |
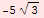 |
-5 |
0 |
c) In order to plot the graph of positions for the time interval [0, T sec], firsty we are calculating T = 

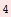
c1) EITHER we are ploting the points (t, x(t) ) for t =0,  ,
,  , 1,
, 1,  ,
, 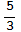 ,2,
,2,  ,
, 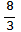 , 3,
, 3, 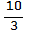 ,
,  ,4 sec from the former table using the command ListPlot[Table[ {t, x [t] }, {t, 0, 4, 1/3} ] ]
,4 sec from the former table using the command ListPlot[Table[ {t, x [t] }, {t, 0, 4, 1/3} ] ]
![[Graphics:../HTMLFiles/Physics, Oscillations_54.gif]](../HTMLFiles/Physics, Oscillations_54.gif)

Taking more points ListPlot[Table[ {t, x [t] }, {t, 0, 4, 0.1} ] ] or ListPlot[Table[ {t, x [t] }, {t, 0, 4, 0.01} ] ]
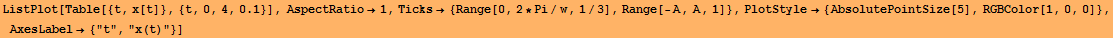
![[Graphics:../HTMLFiles/Physics, Oscillations_57.gif]](../HTMLFiles/Physics, Oscillations_57.gif)
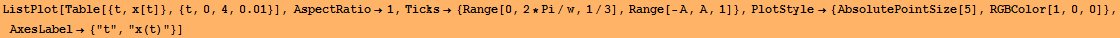
![[Graphics:../HTMLFiles/Physics, Oscillations_60.gif]](../HTMLFiles/Physics, Oscillations_60.gif)

c2) OR we are ploting the graph of the function x(t) for t ∈[0, 4] with the command Plot[x [t], {t, 0, 4} ] ]

![[Graphics:../HTMLFiles/Physics, Oscillations_63.gif]](../HTMLFiles/Physics, Oscillations_63.gif)
EXERCISE:
Using the commands and programs presented above, study the following oscillation:
A body is performing a simple harmonic oscillation, with width A = 5 cm and frequency w = 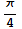 .
.
a) Calculate the position of the body 1, 3 and 7 sec from the starting time point the oscillation (the starting position regarded as 0).
b) Create the table of positions for the time points t = 0, 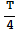 ,
,  ,
, 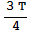 , T,
, T, 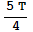 ,
, 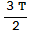 ,
, 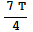 , 2T sec, where T = the smallest period.
, 2T sec, where T = the smallest period.
c) Plot the graph of the position of the body in the time interval [0, 2T sec] .
![[Graphics:../HTMLFiles/Physics, Oscillations_54.gif]](../HTMLFiles/Physics, Oscillations_54.gif)
![[Graphics:../HTMLFiles/Physics, Oscillations_57.gif]](../HTMLFiles/Physics, Oscillations_57.gif)
![[Graphics:../HTMLFiles/Physics, Oscillations_60.gif]](../HTMLFiles/Physics, Oscillations_60.gif)
![[Graphics:../HTMLFiles/Physics, Oscillations_63.gif]](../HTMLFiles/Physics, Oscillations_63.gif)